XZY's BLOG

总结

1. 介绍了数据的分类（数值型、分类型）等；
2. 单变量分析：位置度量（均值、中位数）、变异性度量（方差、标准差、百分位数）等；
3. 单变量的可视化：箱线图、频数表、直方图等；
4. 多变量分析：探索相关性。
5. 多变量的可视化：散点图、热力图、列联表、分类箱线图等；

探索性数据分析（Exploratory Data Analysis，EDA）是数据科学项目的第一步。

数据的分类和主要形式

首先，需要了解数据的分类。在目前世界，数据来源非常丰富，而大多数数据是非结构化的，比如图像、文本、用户交互。这些“信息”，或者说非结构化的数据必须先转化为结构化的数据，才能够用于下一步的分析。

结构化数据的分类：

• 数值型数据
  • 离散型数据：只能取整数；
  • 连续型数据：在一个区间可以取任意值
• 分类型数据
  • 二元数据：两个值中取其一，0 或 1
  • 多元数据
  • 特殊形式：有序数据，按照分类进行排序

需要强调的是，数据的分类对于后续可视化方法的选择、统计模型的选择都非常重要。

接下来需要说明的是数据科学中最经典的引用结构——矩形数据。最常见的就是我们经典的电子表格。其中每一行代表一条观测记录，每一列代表一个特征（变量）。在不同统计编程语言中也有对应的处理方式：

• R语言: data.table
• Python Pandas: DataFrame

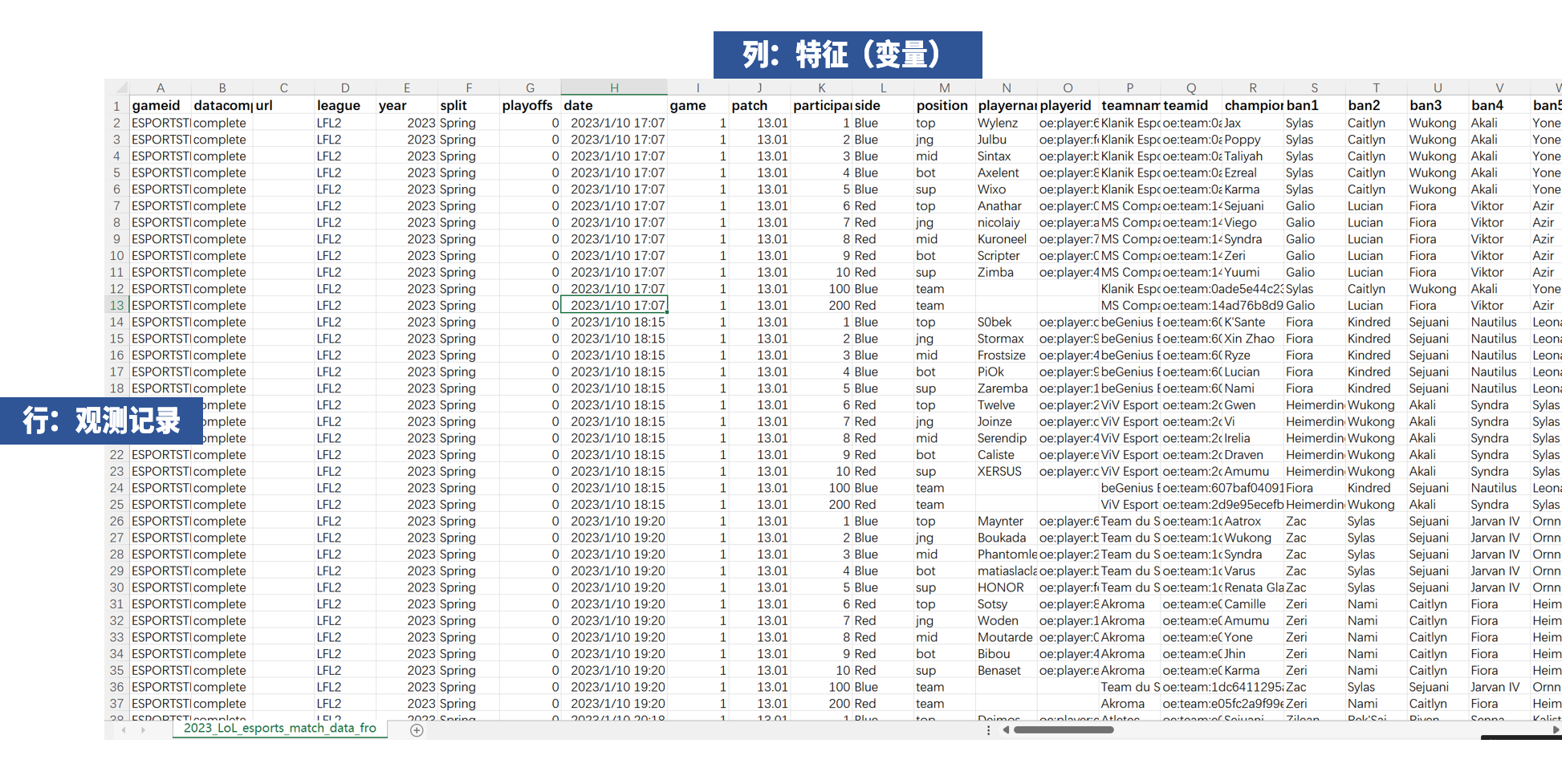
其他的几种非矩形的数据形式包括：时间序列数据、空间数据和图形或网络数据。他们都有对应的处理方法。

如何描述连续性变量？

位置度量

变量代表了测量数据或者计数数据。探索数据的一个基本步骤，就是了解每个变量（特征）的特点。不同种类的数据，我们对其的主要关注点也不尽相同。统计学中主要关注以下数据特征值：

• 均值：基本的位置度量，对极值敏感
• 加权均值：将每个值乘一个权重值然后除以总和
• 切尾均值：消除极值之后的均值，比均值更加稳健
• 中位数：更加稳健，不易受均值影响
• 加权中位数：将数据集排序之后进行加权，加权中位数就是可以使数据集上下两部分的权重总和相同的值
• 离群值：并不一定是无效或错误的数据，但往往是由于数据的错误所导致的。

统计学家替换用估计量（estimate）来表示从手头已有数据计算得到的值，来描述数据情况与真实状态之间的差异。数据科学家和商业分析师更倾向于把这些值称为度量（metric）。因为统计学的核心在于如何解释不确定度，而数据科学则更关注如何解决一个具体的商业或企业目标。

变异性度量

变异性（variability），也称为离差（dispersion），是另外一个描述数据的视角，表示数据是紧密聚集的还是发散的。在分析中主要会考虑：

• 测量数据的变异性；
• 识别各种变异性的来源；
• 如何降低变异性

统计学中有以下数据特征描述变异性：

• 偏差：观测值和估计值之间的直接差异
• 方差
• 标准差：方差的平方根
• 平均绝对偏差：对偏差值取绝对值然后求平均
• 中位数绝对偏差
• 极差：最大值和最小值之间的差值
• 顺序统计量：又称为秩
• 百分位数
• 四分位距（IQR）：75 百分位数和 25 百分位数之间的差值

方差和标准偏差是最广泛使用的变异统计量，且都对离群值敏感。更稳健的度量包括百分位数、四分位距和中位数绝对偏差。

sd (state$Population)
IQR(state$Population)
mad (state$Population)

quantile(state$Murder.Rate, p=c(.05, .25, .5, .75, .95))

使用图表描述数据分布

箱线图

boxplot(state$Population/1000000, ylab="Population (millions)")

箱线图的顶部和底部分别是 75 百分位数和 25 百分位数。水平线代表的是中位数，虚线称为须（whisker） ，从最大值一直延伸到最小值，体现了数据的极差。

频数表

频数表是直方图中频数计数的表格形式。

breaks <- seq(from=min(state$Population), to=max(state$Population), length=11)
pop_freq <- cut(state$Population, breaks=breaks, right=TRUE, include.lowest=TRUE)
table(pop_freq)

组距必须为大小相等的组距，如果组距过大，就会隐藏掉分布的一些重要特性

直方图

直方图在 x 轴上绘制变量值，在 y 轴上绘制频数计数情况，显示了数据的分布。

hist(state$Population, breaks=breaks)

直方图的注意事项：

• 空组距也应该包括在直方图中
• 各个组距是等宽的
• 组距的数量（或大小）取决于用户
• 各个条块应该紧密连接，没有空隙

密度图

密度图通过一条连续的线显示数据值的分布情况，是通过一种核密度估计量直接计算得到的。可以理解为直方图的平滑表示形式。

hist(state$Murder.Rate, freq=FALSE)
lines(density(state$Murder.Rate), lwd=3, col="blue")

如何描述分类数据？

分类数据通常按照比例进行总结，一般使用条形图和饼图进行可视化。

一般描述分类型数据的变量如下：

• 众数：出现次数最多的类别或值；
• 期望值：如果类别和其他数据关联，根据类别出现概率计算的平均值；

探索变量相关性

探索性数据分析中，相关性描述的是两个变量 X 和 Y 之间的相关程度。如果 Y 随着 X 的增大而增大，则 X 和 Y 是正相关的；如果 Y 随着 X 的增大而减小，则 X 和 Y 是负相关的。两者之间没有明显规律，则两个变量之间不相关。

要表示变量之间的相关性，一般使用以下三种工具：

• 相关系数：用于测量相关程度的度量值，取值范围在 -1（完全负相关）到 1（完全正相关）之间；
  • 如果相关系数为0，那么表示两个变量之间没有相关性；
  • 相关系数有不同的几种：皮尔逊相关系数、斯皮尔曼秩相关系数、肯德尔秩相关系数
• 相关矩阵：将变量在一个表格中按行和列显示；
• 散点图：直观表示两个变量之间关系；

相关系数

计算相关系数：

cor(data, method="spearman")

相关矩阵将变量在一个表格中按照行和列进行显示，表格中每个单元格的值是对应变量间的相关性。

library(corrplot)
corrplot(cor(etfs), method="ellipse")

这里要注意：如果两个变量之间的实际关系是非线性的，那么相关系数就不是一个好的度量值。

散点图

散点图是用来可视化两个变量之间关系的标准方法。

plot(data$x, data$y, xlab="x", ylab="y")

除此之外，探索多个变量的不同方法：

• 多个连续型变量：热力图、六边形图
• 多个分类型变量：列联表
• 分类型和数值型变量：分类箱线图、小提琴图

这类类型的图表都可以使用 ggplot2 包完成：

• stat_binhex
• geom_boxplot，geom_violin

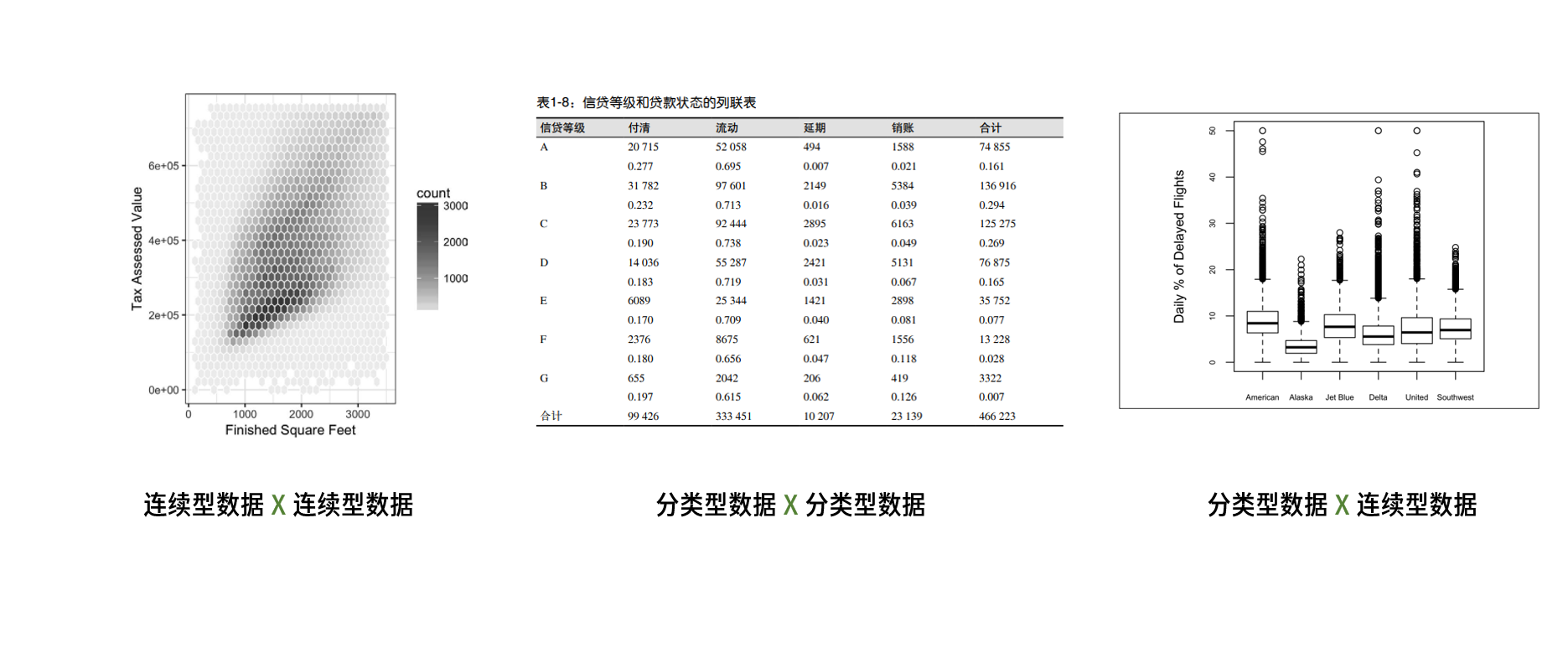
在灵活探索多个变量之间关系的时候，可以考虑关键变量的分组进行显示，比如探索不同人群收入和性别的关系的时候， 可以按照“受教育程度”作为分类进行探索。这里可以使用 facet_wrap，结合 ggplot 进行。