XZY's BLOG

什么是保序回归？

保序回归（Isotonic Regression）是一种适用于单调函数非参数统计回归方法，即在一个序列中，Xn ≥ Xn-1。通过字面理解「Isotonic Regression」：

• iso的意思就是「相等、相同」的意思；
• tonic 就是 tone 的意思，指的是「调」。 所以保序回归的核心还是在于单调递增的函数，当需要分析的数据资料符合单调递增的趋势可以用。

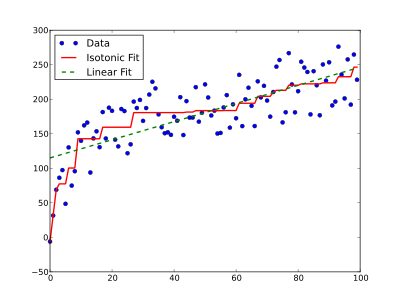
保序回归最常用的应用场景之一是探索药量和药效的关系，因为一般来说药物剂量越高，药效应该更强，因此通过保序回归的方式可以从药效和经济学的角度估计最合适的药量。

保序回归使用 weighted least-squares 来进行拟合：

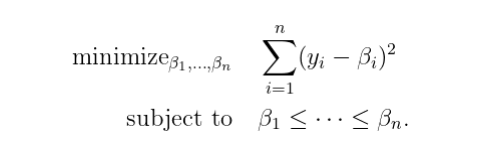
怎么做保序回归？

求解保序回归的一种最常用算法是 PAVA 算法（ Pool-Adjacent-Violators Algorithm，池相邻违规者算法）。PAVA 算法的直观形式只需要看下面这张图就行了：

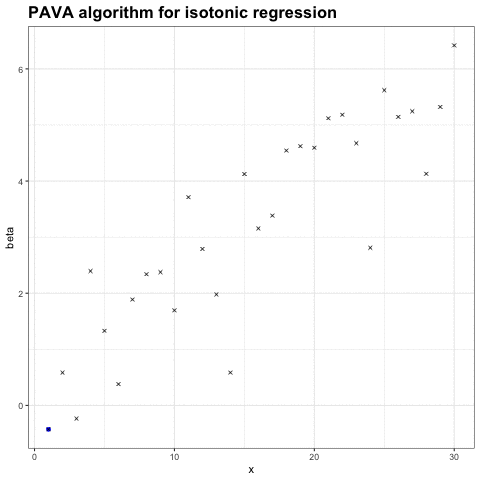
这种算法是通过从左往右逐渐扫描数据序列，并且保证整个序列是单调递增的，以此来获得 Beta 值的结果。如果 Beta_i < Beta_i-1，那么就同时把这两个值替换为 (Beta_i + Beta_i-1) / 2。以此就能获得严格且平滑的保序回归。

通过 PAVA 算法，可以获得一个包括多个 Beta 参数组成的单调递增序列，用可视化的方法可以看到是由多条上升线和水平线组成的函数图：

如何使用 R 语言进行保序回归？

在 R 中可以轻松进行保序回归，只需要使用 stats 包中的 isoreg 函数即可。下面的代码提供一个简单的示例，并将原始数据和拟合值（蓝点）绘制出来。注意，拟合后的蓝点是单调递增的。

# Generate Training Data
set.seed(15)
x <- sample(2 * 1:15)
y <- 0.5 * x + rnorm(length(x))

# Isotonic Regression Model Fit
reg.fit <- isoreg(x, y)

# Isotonic Regression Plot
plot(x, y, pch = 4)
points(reg.fit$x[reg.fit$ord], fit$yf, pch = 16, col = "blue")

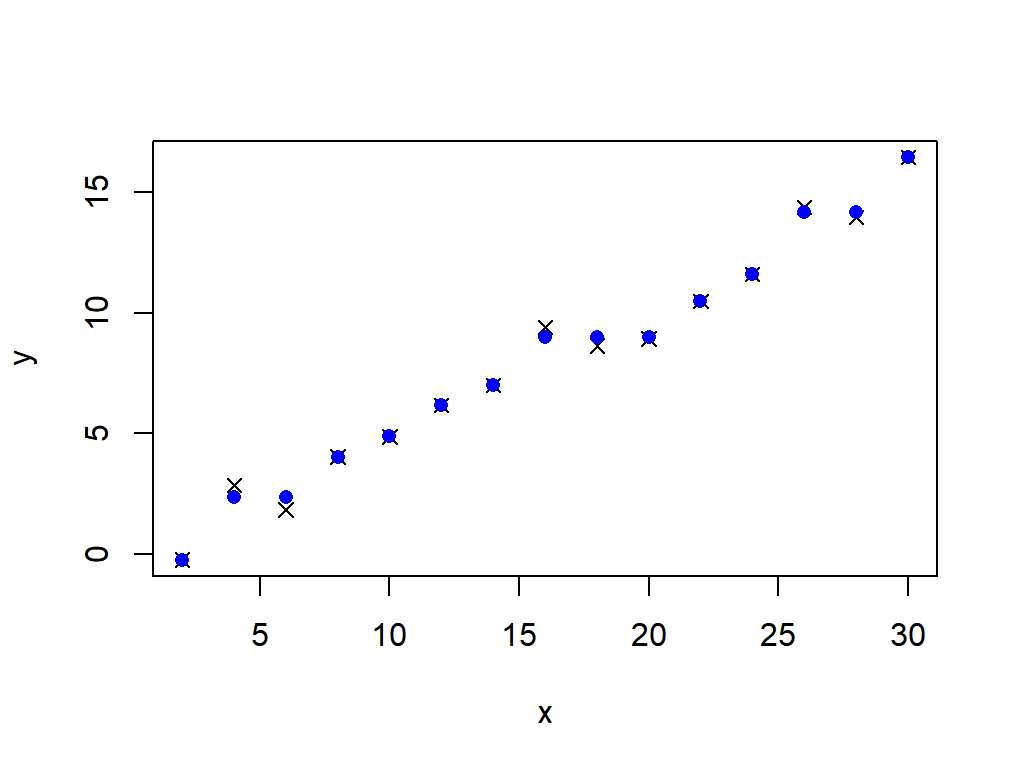
这里需要注意，保序回归模型和其他回归不同的点是，在提取拟合值时，代码语法不同。isoreg 函数的返回值无法和预测数据互动。这里可以考虑使用 sd.stepfun 来完成对预测数据拟合值的校准。代码如下：

# Generate Test Data
test_x <- sample(2 * 1:15 - 1)
test_y <- 0.5 * test_x + rnorm(length(test_x))
all_x <- c(x, test_x)
all_y <- c(y, test_y)

# Isotonic Regression Model Fit
iso.fit <- as.stepfun(isoreg(x, y))

# Predict and Plot
plot(all_x, all_y, pch = 4)
points(all_x, iso.fit(all_x), pch = 15, col = "red")
points(reg.fit$x[reg.fit$ord], reg.fit$yf, pch = 16, col = "blue")

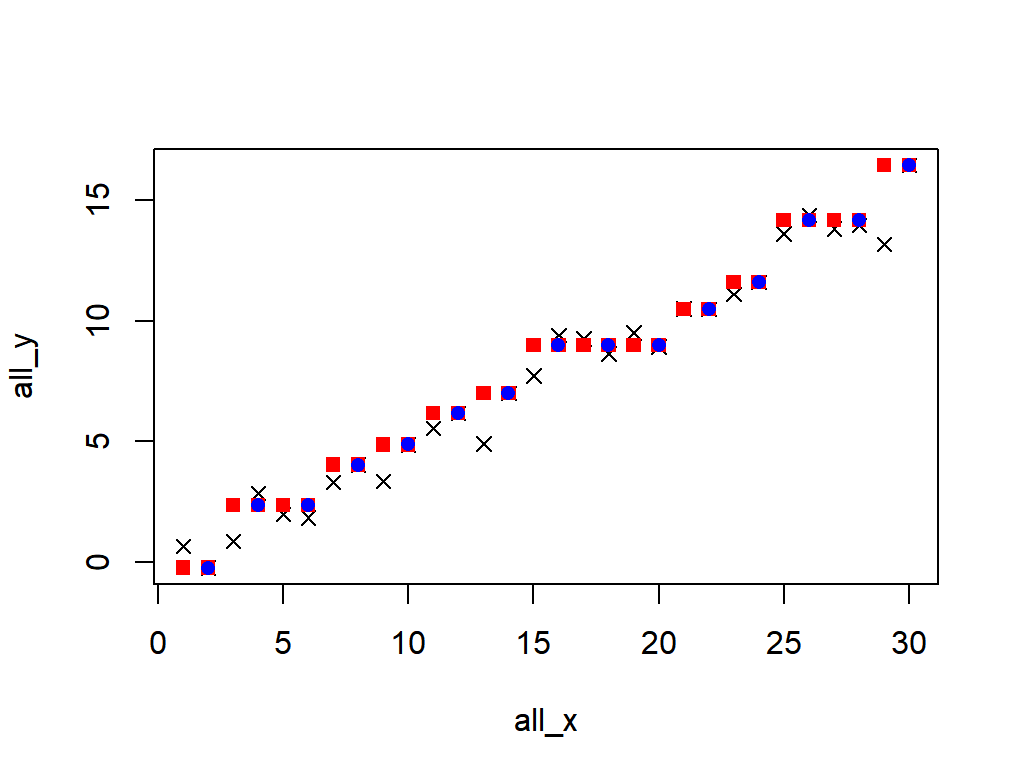
只需要把代码中的 iso.fit 看作是在训练数据上保序回归的拟合得到的黑箱。绘制结果可以显示训练拟合的模型（蓝点）和所有数据的预测值（红点）。可以看到，训练值和拟合值是兼容的，整体拟合依然是单调的。

在 R 语言中使用 PAVA 算法

想要使用 PAVA 算法的话，只需要用 isotone 包下面的 gpava 函数就搞定了，具体文档在此。

使用例子也很简单：

library(isotone)
data(pituitary)
gpava(pituitary[,1],pituitary[,2], ties = "primary")