【医学预测01】Logistic 回归构建变量筛选：先单后多

总结

介绍了 Logistic 回归模型构建过程中的一种变量筛选方式——先单后多；
配合对应的代码实例和结果解释，让方法更加清楚，同时便于日后复习查看。

在 Logistic 回归模型的构建过程中，面对的第一个问题是变量筛选，即筛选哪些作为预测因子进入到最后构建的模型中。其中最为基础的方法是 「先单后多」，顾名思义，即先进行单因素分析，再将单因素分析中具有统计学意义的变量再一起纳入多因素模型中。这样的方法最为简单和实用。

接下来会通过 R 语言代码的实例来演示整个过程。数据采用的是 [Framingham 十年冠心病风险数据](Framingham_CHD_preprocessed_data | Kaggle。

Step 1 数据的读取和预处理

第一步，当然是读取数据并且通过 names 、summary 和 str 分别查看数据集的变量名称、基本统计信息和变量的类型。尤其是后两者，能够提供变量的数据类型和统计信息，有助于发现异常的数据，在分析之前发现原因提前纠正。

# 导入数据，命名为 data
library(readr)

data <- read_csv("framingham.csv")

# 查看变量名称
names(data)

# 查看基本统计信息
summary(data)

# 查看变量类型
str(data)

接下来对数据做基础的预处理。对于医学数据，需要注意的预处理主要是对于分类变量的转换：

将分类变量转换为 factor；
二分类变量处理或者不处理不影响结果，多分类变量则一定要进行处理，为了保险和便利起见，尽量都进行处理；
转换中，使用 labels 标清楚各个分类代表的含义，之后不容易发生混淆。

# 标明连续型变量和分类型变量
contin_vars <- c("age", "cigsPerDay", "totChol", "sysBP", "diaBP", "BMI", "heartRate", "glucose")
discre_vars <- c("male", "education", "currentSmoker", "BPMeds", "prevalentStroke", "prevalentHyp", "diabetes")

# 处理分类变量
data$TenYearCHD <- factor(data$TenYearCHD, levels=c(0, 1), 
                          labels = c("未来10年无冠心病风险", "未来10年具有冠心病风险"))

data[discre_vars] <- lapply(data[discre_vars], factor)

Step 2 单因素分析

一般而言，单因素可以采用的统计分析方法包括：t 检验、卡方检验和秩和检验。t 检验需要满足数据符合正态分布，如果不满足则需要考虑秩和检验这种非参数检验。另外卡方检验则一般面向分类的数据，而非定量数据，比如性别（1代表男，2代表女，数字无比较意义）。

# 对连续变量进行 t 检验
# 对分类变量进行卡方检验
library(tableone)
table1 <- CreateTableOne(vars=c(contin_vars, discre_vars),
                         data=data,
                         factorVars=discre_vars,
                         strata="TenYearCHD", addOverall=FALSE)
result1 <- print(table1, showAllLevels=FALSE)
write.csv(result1, "result1.csv")

这时，可以看到 tableone 的输出结果。可以看到，按照连续型变量和分类变量展示了不同统计结果（Mean(SD)/占比）。并且在最后一列给出了统计学的检验结果 P 值。

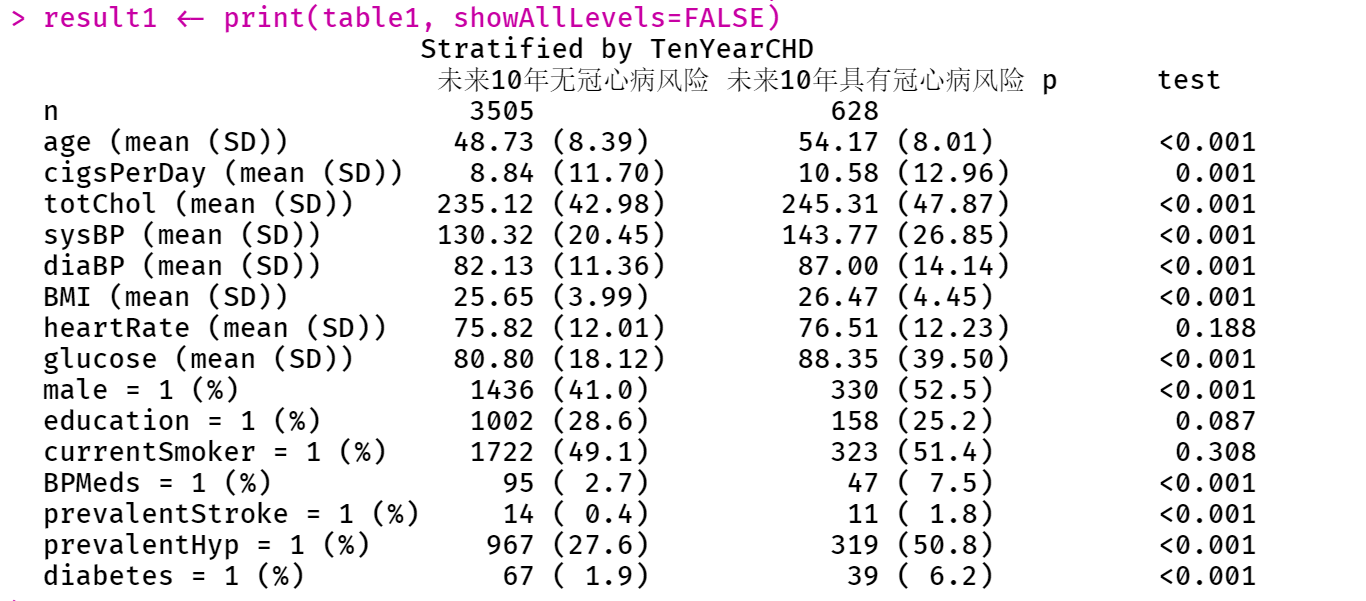
这里可以补充几个参数的说明：

addOverall：在列上展示所有出 Overall 的情况。
showAllLevels：如果设置为 TRUE，展示所有变量的所有水平；
nonnormal：不满足正态条件，可以指定确切进行秩和检验的变量，之后在结果会显示中位数、第一四分位数和第三四分位数；
exact：不满足卡方条件，可以指定确切概率检验的变量。

Step 3 单因素的 Logistic 模型分析

在完成上述分析之后，可以开始进行多因素模型构建。有时，我们会先进行单因素的 Logistic 模型分析，然后再做多因素的 Logistic 模型构建。这样的好处在于，我们可以观察到对于某个单个变量的 Crude OR值（俗称的粗 OR值）和调整后 OR 值（adjustment OR）。

这里举一个变量的例子：

# 单因素 logistic
# 如果存在分类变量，需要设置哑变量

# 自变量: 年龄
model <- glm(TenYearCHD~age, data=data, family=binomial())
summary(model)
summary(model)$coefficients
# 计算 OR 及其可信区间
exp(cbind("OR"=coef(model), confint(model)))

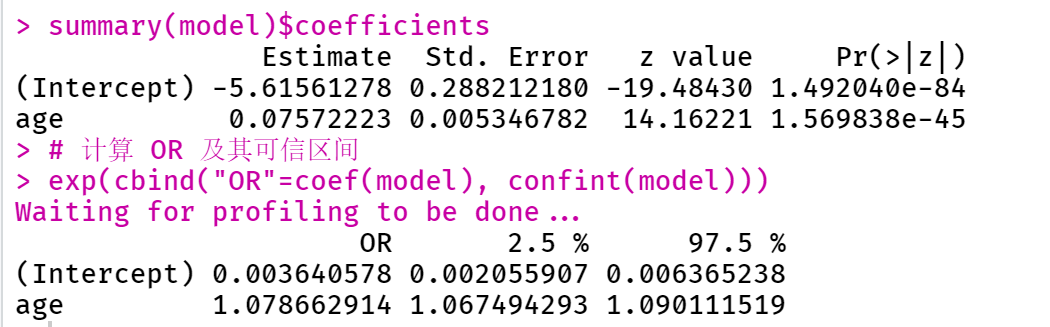
这里结果显示了自变量 age 的参数值、标准误、z 值以及 P 值。可以看到，P 值明显小于 0.05，说明「年龄」这个自变量在单因素 Logistic 回归里是有意义的。

再来看下面的 OR 值，为 1.079 (1.067, 1.090)，可以解释为，年龄每增加 1 岁，未来10年的冠心病发生风险是之前的 1.079 倍。

对于一个分类变量「糖尿病」来说：

# 自变量: 糖尿病合并症
model <- glm(TenYearCHD~diabetes, data=data, family=binomial())
summary(model)
summary(model)$coefficients
# 计算 OR 及其可信区间
exp(cbind("OR"=coef(model), confint(model)))

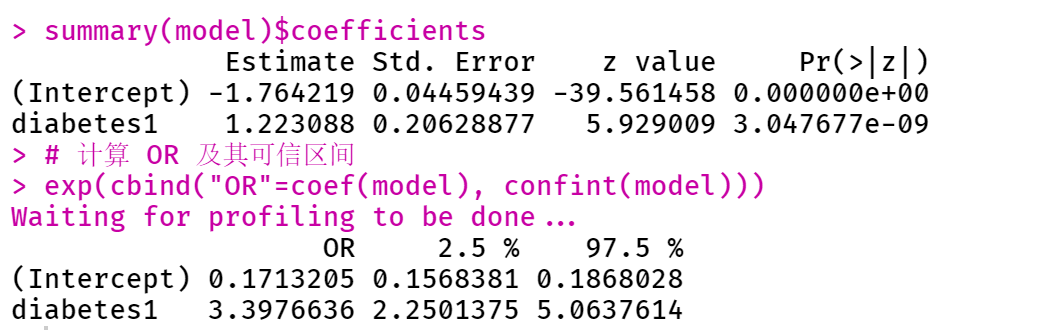
与上述同理，不过这里的 OR 值 3.398 (2.250, 5.064) 可以解释为，具有糖尿病合并症人群未来 10 年的冠心病发生风险是无糖尿病人群的 3.398 倍。

Step 4 多因素的 Logistic 模型分析

常规方式

根据上面单因素分析的结果，如果某变量的 P 值一般小于 0.05，就可以将该变量纳入多因素模型中。实际应用中，也可以将纳入标准放宽，即 P 值小于 0.1，就纳入多因素模型。

# 多因素模型分析
model <- glm(TenYearCHD~var1+var2+var3+...+varn, data=data, family=binomial())
summary(model)$coefficients
exp(cbind("OR"=cord(model), confint(model)))

这里就不展示结果了。得到的 OR 值可以认为是调整后的 OR 值。解释的结果和上面也大同小异。

有时候会发现，部分之前单因素分析时存在统计学意义的变量，在多因素中则不存在统计学意义。这很可能是因为存在混杂偏倚，而多因素分析在一定程度上控制了混杂偏倚。

另一种非常规的方式

假如我们已经确定了要研究的是某个因素（就叫做主因素吧）和因变量，也就是结局之间的关系，我们应该如何筛选协变量呢？

如果某个协变量与因变量之间单因素分析的 P 值小于 0.1，并且当纳入主因素和协变量同时进行分析后，由于协变量的存在，主因素的系数相比之前只有主因素时，变化超过了 10%，那么就说明这个协变量其实是对主因素的系数有一定程度的影响，应该纳入到多因素分析中。这里可以采用下面的代码：

uni_methods <- function(xvar) {
  model <- glm(TenYearCHD~diabetes, data=data, family=binomial())
  coef <- coef(model)[2]
  form <- as.formula(paste0("TenYearCHD~diabetes+", xvar))
  model2 <- glm(form, data=data, family=binomial())
  coef2 <- coef2(model2)[2]
  ratio <- abs(coef2-coef1)/coef1
  if (ratio > 0.1) {
    return(xvar)
  }
}

xvar <- c(contin_vars, discre_vars)
xvar <- xvar[-which(xvar=="diabetes")]
lapply(xvar, uni_methods)

这里我们确定变量 diabetes 作为我们的主因素，然后筛选其他协变量。只要 ratio ，也就是系数的变化幅度大于 10%，就可以在最后的结果中显示出来。

XZY's BLOG